Degrees Conferred by Major ( ) Source: National Center for Education Statistics (NCES) Business 366,815 Social Sciences 178,543 Psychology 108, ppt download
Mathematics in the 18 th Century Pierre LaPlace ( ) Leonhard Euler ( ) Johann Gauss ( ) Joseph Fourier ( ) Brook Taylor ( )
Degrees Conferred by Major ( ) Source: National Center for Education Statistics (NCES) Business 366,815 Social Sciences 178,543 Psychology 108,986 Education 105,785 Biology 95,849 Visual and Performing Arts 95,749 Journalism Communication 88,752 English 53,767 Computer Sciences 47,304 Foreign Language 21,764 Mathematics 18,842 Chemistry 13,472 Engineering 7,028 Physics 5,531
Thomson ( ) Ludwig Boltzmann ( ) J. W. Gibbs ( ).
The motions of gas particles are completely random. Motion is tied to heat energy content 3b. The average energy of particles increases with temperature. 4. Collisions between particles or with container walls are elastic. Kinetic energy and momentum are conserved The Ideal Gas 1. Gas particles are charge-less objects with no internal structure 3a. The average speed of particles increases with temperature..
Gauge Pressure – referenced against atmospheric pressure. Differential Pressure – difference in pressure between two points..
Pressure Force Area m = V h A m = h A P = g h Height of a column of Hg exerting pressure equal to atmospheric pressure : Evangelista Torricelli density Pressure exerted by a column of fluid is independent of its surface area.
Pressure vacuumsealed tube absolute pressure 1380 mm Hg open tube gauge pressure 620 mm Hg P(air) = 760 mm Hg absolute pressure = 1380 mm Hg P 1 = g h 1 P 2 = g h 2 Differential Pressure: fluid g (h 2 - h 1 ) = fluid g l h1h1 h2h2 l If the cube faces have area A then the buoyancy force is B =(P 2 - P 1 ) A = fluid g l A = fluid g V Since: m fluid = fluid V the buoyancy force is proportional to the mass of fluid displaced by the object The object exerts downward force: F = m object g = object V g If: fluid > object the buoyancy force is greater than the downward force and the object floats
+x Only those particles possessing velocities in the positive x- direction will exert pressure on that wall..
The change in momentum each particle undergoes is: p x = mv x – (-mv x ) = 2mv x During a time interval t only a certain fraction of the gas particles strike the wall..
+x vxtvxt A If the wall has area A, all particles in a volume A v x t will reach the wall. The number density of gas particles is nN A /V where n is the moles of gas and N A is Avogadro’s number. At any instant, ½ the particles are heading towards the right. Total momentum change: Gas Pressure and Gas Particle Speed (Ch 1, pp 10-13) molar mass of the gas (M = mN A ) gas densitynumber striking wall momentum change.
Gas Pressure and Gas Particle Speed (Ch 1, pp 10-13) Pressure exerted by gas particles in the x-direction: Mean speed of gas particles in c 2 = v x 2 + v y 2 + v z 2 = 3v x 2 all directions: Total momentum change: Pressure contribution of all gas particles: The kinetic temperature of the gas is related to the root mean square speed: Rearrange and insert: PV = nRT
Gas RMS Speeds at Room Temperature (298 K) He (molar mass kg mol -1 ): 1,360 m s -1 (3,240 MPH) N 2 (molar mass kg mol -1 ): 515 m s -1 (1,230 MPH) O 2 (molar mass kg mol -1 ): 482 m s -1 (1,150 MPH) Speed of sound in air: 340 m s -1 (811 MPH)
The Distribution of Speeds In a gas sample, the particles are instantaneously moving at a wide variety of velocities These individual velocities can be collectively averaged in a variety of statistical ways.
discrete distribution continuous distribution.
James Clerk Maxwell Fraction with speeds between v 1 and v 2 : Distribution over all possible speeds found using:.
Distribution Function Justification (Ch 6 pp ) Components of the velocity distribution are independent of one other Using the definition of molecular speed If the distribution depends only on speed but not direction Negative exponential so that probability of extremely high velocities is small Therefore because e (x + y + x) = e x e y e z N found by imposing normalization
Distribution Function Justification (Ch 6 pp ) Using the definition of mean square speed We have previously found the mean speed Inserting this result To evaluate , we first use the function to find the mean square speed There is equal probability of v x, v y, or v z velocities, so the 3-d form is the cube f(v x )
Distribution Function Justification (Ch 6 pp ) Inserting the volume element gives the Maxwell distribution function 3-dimensional velocity space can be represented in the same fashion as spherical polar coordinates: Integrating the angular components of the volume element The same result was also derived using Boltzmann’s statistical mechanical partition function, so this is called the Maxwell-Boltzmann distribution of speeds.
Maxwell Distribution of Speeds for Neon at 450 K f (v) v ( m/s) Total 0.999
f(v)f(v) v( m/s) Distribution of Speeds for Gases at Room Temperature The Maxwell Distribution of Speeds O2O2 CH 4 He f(v)f(v) v( m/s) Distribution of Speeds for CO 2 at Various Temperatures 150 K 750 K 1800 K
Mean speed: use: For Neon at 450 K, = 689 m/s.
Averaged Velocities Using the Distribution Function Mean square speed: use: For Neon at 450 K, c = 747 m/s rms speed:
Most Probable Speed f (v) v For Neon at 450 K c * = 610 m/s
The gas system exerts an internal pressure on the walls of the container. According to Newton’s 3 rd law, the walls exert an equal and opposite pressure back on the gas system. A variable-wall container creates a constant-pressure, or isobaric system. The gas system exerts an internal pressure on the walls of the container that is exactly matched by the external ambient pressure..
Low pressure High pressure P 1 V=n 1 RT P 2 V=n 2 RT.
PV 1 =n 1 RT PV 2 =n 2 RT Amedeo Avogadro Avogadro’s Law.
Low external pressure High external pressure Robert Boyle P 1 V 1 =nRT P 2 V 2 =nRT P1V1 =P2V2P1V1 =P2V2 Boyle’s Law.
V Plot P (atm) V (L) Plot of Pressure vs Volume 200 K 800 K 1500 K Slope of the plot: Negative slope non-linear in V.
Inverse Volume 200 K 800 K 1500 K Slope of the plot: what is: . Variable transformation: For a closed system undergoing isothermal expansion, the slope of a P-1/V plot is constant, positive, and increases with T.
Below the critical temperature the isotherms are discontinuous. Pressure Volume At high temperatures, real gas isotherms appear ideal. Vapor Liquid 2 Phase Region Below the critical temperature real gases condense..
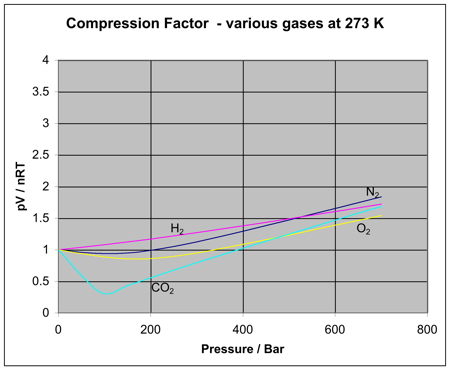
Substituting the ideal molar volume into the compression factor equation we find: Which rearranges to: PV m = RTZ Real gases can have Z values that deviate positively or negatively from 1. The deviation from 1 indicates the imperfection of the real gas..
Power Series in Pressure PV m = RT(1 + B´P + C´P 2 + D´P 3 + …) Power Series in Volume If these are converging power series: D << C << B << 1 In terms of the compression factor: 4 th 3 rd 2 nd 3 rd 4 th virial coefficients 1 st 1 st virial coefficient A = A =1 Z = 1 + B´P + C´P 2 + D´P 3 + ….
Virial Coefficients and The Taylor Series Expansion Taylor Series: Brook Taylor st virial coefficient: 2 nd virial coefficient: PV m = RT(1 + B´P + C´P 2 + D´P 3 + …) Virial Expansion: Rewrite expansion:
Virial Coefficients and The Taylor Series Expansion 3 rd virial coefficient: 4 th virial coefficient: Similarly for: 1/V m 0 as V m
rearranged: Substancea (atm L 2 /mole 2 )b (L/mole) Ar CO He Xe
What is the pressure of CO 2 behaving as a v.d.W. gas when it has a molar volume of 22.4 L/mole .
P – 1/V Plots of CO2 as an Ideal Gas and a vdW Gas Models agree in the low pressure (high volume) limit Models vary dramatically in the high pressure (low volume) limit
Boyles Law and the vdW Equation The vdW equation Perform two experiments where pressure and volume are allowed to vary in an isothermal, closed system; Because the right-hand side of both eqs are equal; In terms of molar volume;
Other Real Gas Models Used Alternative to the vdW Berthelot: Dieterici: Peng-Robinson:
Comparing the Virial and vdW Eqs of State (Prob 1.17c) Expand the first term using: Compare to virial expansion: Express in form of compression factor:
Virial Coefficients from Direct Differentiation of vdW Change of variable for differentiation combining 1 st two terms
Virial Coefficients from Direct Differentiation of vdW The second virial coefficient The first term is in an indeterminate form Successive applications of L’Hôpital’s rule Substitution leads to the vdW form of the second virial coefficient L’Hôpital’s rule Guillaume de L’Hôpital ( )

College Students Are Pursuing Science and Technology Degrees More

State of the Education Data Infrastructure: What Three Experts

DISS (Disciplines within Social Sciences)

DISS (Disciplines within Social Sciences)
Field of degree: Social science : Occupational Outlook Handbook

National Center for Education Statistics (NCES)

Statistics for the Social Sciences - ppt download

DISS (Disciplines within Social Sciences)

National Center for Education Statistics - NCES

DISS (Disciplines within Social Sciences)

DISS (Disciplines within Social Sciences)

3 measures of central dendency

Degrees Conferred by Major ( ) Source: National Center for Education Statistics (NCES) Business 366,815 Social Sciences 178,543 Psychology 108, ppt download

COE - Undergraduate Degree Fields